Ну вот и подошли к концу новогодние каникулы, а с ними и мое обучение по C++. Как говорил, закончил его с отличием. Сегодня рассмотрим задачи с использованием функций. Часть задач будет решаться с использованием рекурсивных функций. Напомню, что эти задачи рассматривались в курсе Введение в программирование (С++) на сайте steptic.org. Сейчас немного поделюсь новостями, а потом приступим к задачам.

Немного доработал сайт

• Сделал рубрикатор, за одно переделал состав рубрик. Добавил ссылку на рубрики на главную страницу.
• Немного доработал лайки. Теперь зарегистрированные пользователи не смогут их накрутить. Пока оставил возможность ставить лайки незарегистрированным пользователям, но теперь без возможности накрутки. Пришлось обнулить все лайки к статьям для функционирования новой механики.
• Сделал еще несколько небольших улучшений и поправил несколько ошибок.
• Регистрацию так и не удалось побороть, так что лучше регистрироваться через социальные сети. 

Задача №1

Напишите функцию min(a, b), вычисляющую минимум двух чисел. Затем напишите функцию min4(a, b, c, d), вычисляющую минимум 4 чисел с помощью функции min. Считайте четыре целых числа и выведите их минимум.
Формат входных данных
Вводятся четыре целых числа.
Формат выходных данных
Выведите ответ на задачу.

Sample Input:
4 5 6 7
Sample Output:
4

#include <iostream>
using namespace std;

int min(int a, int b) {
    if (a < b) return a;
    else return b;
}

int main() {
    int a, b, c , d;
    cin >> a >> b >> c >> d;
    cout << min(min(a,b), min(c,d));
    return 0;
}

Задача №2

Даны четыре действительных числа: $%x_1$%, $%y_1$%, $%x_2$%, $%y_2$%. Напишите функцию distance(x1, y1, x2, y2), вычисляющую расстояние между точкой $%(x_1, y_1)$% и $%(x_2, y_2)$%. Считайте четыре действительных числа и выведите результат работы этой функции.
Формат входных данных
Вводятся четыре действительных числа.
Формат выходных данных
Выведите ответ на задачу.

Sample Input:
0 0 1 1
Sample Output:
1.41421

#include <iostream>
#include <iomanip>
#include <cmath>

using namespace std;
double distance(double x1, double y1, double x2, double y2) {
    double a = abs(x1 - x2);
    double b = abs(y1 - y2);
    return sqrt(a*a + b*b);
}

int main() {
    double  x1, y1,  x2, y2;
    cin >> x1 >> y1 >> x2 >> y2;
    cout << fixed << setprecision(5);
    cout << distance(x1, y1, x2, y2);
    return 0;
}

Задача №3

Даны два действительных числа $%x$% и $%y$%. Проверьте, принадлежит ли точка с координатами $%(x, y)$% заштрихованному квадрату (включая его границу). Если точка принадлежит квадрату, выведите слово YES, иначе выведите слово NO.

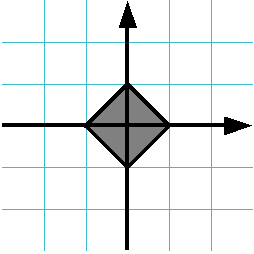
На рисунке сетка проведена с шагом 1.
Решение должно содержать функцию IsPointInSquare(x, y), возвращающую true, если точка принадлежит квадрату и false, если не принадлежит. Основная программа должна считать координаты точки, вызвать функцию IsPointInSquare и в зависимости от возвращенного значения вывести на экран необходимое сообщение.
Функция IsPointInSquare не должна содержать инструкцию if.
Формат входных данных
Вводятся два действительных числа.
Формат выходных данных
Выведите ответ на задачу.

Sample Input 1:
0 0
Sample Output 1:
YES

Sample Input 2:
3 -7
Sample Output 2:
NO

#include <iostream>
#include <cmath>
using namespace std;

bool IsPointInSquare(double x, double y) {
    return abs(x) + abs(y) <= 1;
}

int main() {
    double  x, y;
    cin >> x >> y;
    if (IsPointInSquare(x, y)) {
        cout << "YES";
    }
    else
        cout << "NO";
    return 0;
}

Задача №4

Даны пять действительных чисел: $%x$%, $%y$%, $%x_c$%, $%y_c$%, $%r$%. Проверьте, принадлежит ли точка $%(x, y)$% кругу с центром $%(x_c, y_c)$% и радиусом $%r$%. Если точка принадлежит кругу, выведите слово YES, иначе выведите слово NO.
Решение должно содержать функцию IsPointInCircle(x, y, xc, yc, r), возвращающую True, если точка принадлежит кругу и False, если не принадлежит.
Основная программа должна считать координаты точки, вызвать функцию IsPointInCircle и в зависимости от возвращенного значения вывести на экран необходимое сообщение.
Функция IsPointInCircle не должна содержать инструкцию if.
Формат входных данных
Вводятся пять действительных чисел.
Формат выходных данных
Выведите ответ на задачу.

Sample Input 1:
0.5
0.5
0
0
1
Sample Output 1:
YES

Sample Input 2:
0.5
0.5
1
1
0.1
Sample Output 2:
NO

#include <iostream>
#include <cmath>

using namespace std;

bool IsPointInCircle(double x, double y, double xc, double yc, double r) {
    return abs(x - xc)*abs(x - xc) + abs(y - yc)*abs(y - yc) <= r*r;
}

int main() {
    double  x, y, xc, yc, r;
    cin >> x >> y >> xc >> yc >> r;
    if (IsPointInCircle(x, y, xc, yc, r)) {
        cout << "YES";
    }
    else
        cout << "NO";
    return 0;
}

Задача №5

Проверьте, принадлежит ли точка данной закрашенной области:

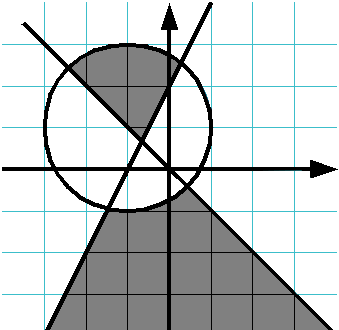
Если точка принадлежит области (область включает границы), выведите слово YES, иначе выведите слово NO.
Решение должно содержать функцию IsPointInArea(x, y), возвращающую True, если точка принадлежит области и False, если не принадлежит. Основная программа должна считать координаты точки, вызвать функцию IsPointInArea и в зависимости от возвращенного значения вывести на экран необходимое сообщение.
Функция IsPointInArea не должна содержать инструкцию if.
Формат входных данных
Вводятся два действительных числа.
Формат выходных данных
Выведите ответ на задачу.

Sample Input 1:
-4 -4
Sample Output 1:
NO

Sample Input 2:
-4 -3
Sample Output 2:
NO

#include <iostream>
#include <cmath>

using namespace std;

bool IsPointInArea(double x, double y) {
    double in_circle = 2 * 2 >= abs(x + 1) * abs(x + 1) + abs(y - 1) * abs(y - 1);
    double above_line1 = y >= 2 * x + 2;
    double above_line2 = y >= -x;
    double below_line1 = y <= 2 * x + 2;
    double below_line2 = y <= -x;
    double on_circle = 2 * 2 == abs(x + 1) * abs(x + 1) + abs(y - 1) * abs(y - 1);

    return in_circle && above_line1 && above_line2 || (on_circle || not in_circle) && below_line1 && below_line2;
}

int main() {
    double  x, y;
    cin >> x >> y;

    if (IsPointInArea(x, y)) cout << "YES";
    else cout << "NO";
    return 0;
}

Задача №6

Дано действительное положительное число $%a$% и целоe число $%n$%. Вычислите $%a^n$%. Решение оформите в виде функции power(a, n).
Формат входных данных
Вводится действительное положительное число $%a$% и целоe число $%n$%.
Формат выходных данных
Выведите ответ на задачу.

Sample Input 1:
2 1
Sample Output 1:
2

Sample Input 2:
2 2
Sample Output 2:
4

#include <iostream>
#include <cmath>
#include <iomanip>

using namespace std;

double power(double a, int n) {
    double p;
    if (n == 0) p = 1;
    else if (n == 1) p = a;
    else if (n > 1) {
        p = a;
        for (int i = 2; i <= n; i++) p = p * a;
    }
    else if (n < 0) {
        p = a;
        for (int i = 2; i <= -n; i++) p = p * a;
        p = 1 / p;
    }
    return p;
}

int main() {
    double  a;
    int n;
    cin >> a >> n;
    cout << fixed << setprecision(5);
    cout << power(a,n);
    return 0;
}

Задача №7

Дано натуральное число $%n > 1$%. Выведите его наименьший делитель, отличный от 1.
Решение оформите в виде функции MinDivisor(n). Количество операций в программе должно быть пропорционально $%sqrt{n}$%.
Указание
Если у числа $%n$% нет делителя, меньшего $%n$% , то число $%n$% — простое и ответом будет само число $%n$%.
Формат входных данных
Вводится натуральное число.
Формат выходных данных
Выведите ответ на задачу.

Sample Input 1:
4
Sample Output 1:
2

Sample Input 2:
5
Sample Output 2:
5

#include <iostream>
#include <cmath>

using namespace std;

int MinDivisor(int n) {
    int min_divisor = 1;
    int sqrt_n = sqrt((double)n);
    for (int i = 2; i <= sqrt_n; i++) {
        if (n % i == 0)
        {
            min_divisor = i;
            break;
        }
    }
    if (min_divisor == 1)
        return n;
    else
        return min_divisor;
}

int main() {
    int n;
    cin >> n;
    cout << MinDivisor(n);

    return 0;
}

Задача №8

Дано натуральное число $%n > 1$%. Проверьте, является ли оно простым. Программа должна вывести слово YES, если число простое и NO, если число составное.
Решение оформите в виде функции IsPrime(n), которая возвращает True для простых чисел и False для составных чисел. Количество операций в программе должно быть пропорционально $%/sqrt{n}$%.
Формат входных данных
Вводится натуральное число.
Формат выходных данных
Выведите ответ на задачу.

Sample Input 1:
2
Sample Output 1:
YES

Sample Input 2:
4
Sample Output 2:
NO

#include <iostream>
#include <cmath>

using namespace std;

bool IsPrime(int n) {
    int min_divisor = 1;
    int sqrt_n = sqrt((double)n);
    for (int i = 2; i <= sqrt_n; i++) {
        if (n % i == 0)
        {
            min_divisor = i;
            break;
        }
    }
    if (min_divisor == 1)
        return true;
    else
        return false;
}

int main() {
    int n;
    cin >> n;
    if (IsPrime(n)) cout << "YES";
    else cout << "NO";
    return 0;
}

Задача №9

Возводить в степень можно гораздо быстрее, чем за $%n$% умножений! Для этого нужно воспользоваться следующими рекуррентными соотношениями:
$%a^n = (a^2)^{n/2}$%, при четном $%n$%,
$%a^n = a × a^{n-1}$%, при нечетном $%n$%

Реализуйте алгоритм быстрого возведения в степень с помощью рекурсивной функции.
Формат входных данных
Вводятся действительное число a и целое неотрицательное число $%n$%.
Формат выходных данных
Выведите ответ на задачу.

Sample Input 1:
2.0
1
Sample Output 1:
2

Sample Input 2:
2
2
Sample Output 2:
4

#include <iostream>
#include <iomanip>
using namespace std;

double power(double a, int n) {
    if (n == 0) return 1;
    if (n % 2 == 0) return power(a*a, n/2);
    return a * power(a, n - 1);
}

int main() {
    double  a;
    int n;
    cin >> a >> n;
    cout << fixed << setprecision(5);
    cout << power(a,n);
    return 0;
}

Задача №10

Дана последовательность чисел, завершающаяся числом 0. Найдите сумму всех этих чисел, не используя цикл.
Формат входных данных
Вводится последовательность целых чисел, оканчивающаяся числом 0 (само число 0 в последовательность не входит, а служит как признак ее окончания).
Формат выходных данных
Выведите ответ на задачу.

Sample Input:
1 7 9 0
Sample Output:
17

#include <iostream>
#include <iomanip>
using namespace std;

int sum() {
    int n;
    cin >> n;
    if (n == 0) return 0;
    return n + sum();
}

int main() {
    cout << sum();
    return 0;
}

Задача №11

Напишите функцию fib(n), которая по данному целому неотрицательному $%n$% возвращает $%n$%-e число Фибоначчи. В этой задаче нельзя использовать циклы - используйте рекурсию.
Первое и второе числа Фибоначчи равны 1, а каждое следующее равно сумме двух предыдущих.
Формат входных данных
Вводится целое число.
Формат выходных данных
Выведите ответ на задачу.

Sample Input:
1
Sample Output:
1

#include <iostream>
using namespace std;

int fib(int n) {
    if (n == 0) return 1;
    if (n == 1) return 1;
    if (n == 2) return 1;
    return fib(n - 1) + fib(n - 2);
}

int main() {
    int n;
    cin >> n;
    cout << fib(n);
    return 0;
}

Задача №12

Дано число N. Определите, сколькими способами можно расставить на доске $%N×N$% $%N$% ферзей, не бьющих друг друга.
Формат входных данных
Задано единственное число $%N$%. $%(N ≤ 10)$%
Формат выходных данных
Выведите ответ на задачу.

Sample Input:
8
Sample Output:
92

#include <iostream>
using namespace std;

int board[10];

bool check(int i, int j, int k) {
    if (k == i) return true;
    else return board[k] != j && (i - k) != (j - board[k]) && (i - k) != (board[k] - j) && check(i, j, k + 1);
}

int put_queen(int n, int i, int j) {
    if (i == n) return 1;
    else {
        if (j < n) {
            int r = 0;
            if (check(i, j, 0)) {
                board[i] = j;
                r = put_queen(n, i + 1, 0);
            }
            return r + put_queen(n, i, j + 1);
        }
        else return 0;
    }
}

int main() {
    int n;
    cin >> n;
    cout << put_queen(n, 0, 0);
    return 0;
}