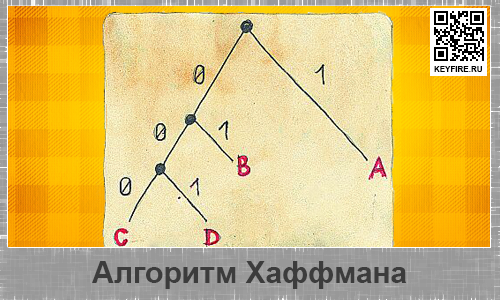
Сегодня рассмотрим задачу по кодированию строки по алгоритму Хаффмана и ее декодированию. Также в ходе решения задачи будет рассмотрен тест алгоритма, позволяющий оценить его корректность. Условие задачи:

По данной непустой строке $%s$% длины не более $%10^4$%, состоящей из строчных букв латинского алфавита, постройте оптимальный беспрефиксный код. В первой строке выведите количество различных букв $%k$%, встречающихся в строке, и размер получившейся закодированной строки. В следующих $%k$% строках запишите коды букв в формате $%"letter: code"$%. В последней строке выведите закодированную строку.

Sample Input:
abacabad

Sample Output:
4 14
a: 0
b: 10
c: 110
d: 111
01001100100111

Алгоритм Хаффмана основан на использовании информации о частотах вхождения символов в строку. В рассмотренном ниже примере будет показано:

• кодирование символов на основании частоты
• получение кодированной строки
• декорирование строки
• тестирование алгоритма

Для алгоритма со временем работы $%O(nlogn)$% будем использовать очередь с приоритетами. Кому лень читать все что написано ниже, можно просто посмотреть визуализацию. Наже приведен алгоритм кодирования на Python:

import heapq  # модуль для работы с мин. кучей из стандартной библиотеки Python
from collections import Counter  # словарь в котором для каждого объекта поддерживается счетчик
from collections import namedtuple

# добавим классы для хранения информации о структуре дерева
# воспользуемся функцией namedtuple из стандартной библиотеки
class Node(namedtuple("Node", ["left", "right"])):  # класс для ветвей дерева - внутренних узлов; у них есть потомки
    def walk(self, code, acc):
        # чтобы обойти дерево нам нужно:
        self.left.walk(code, acc + "0")  # пойти в левого потомка, добавив к префиксу "0"
        self.right.walk(code, acc + "1")  # затем пойти в правого потомка, добавив к префиксу "1"

class Leaf(namedtuple("Leaf", ["char"])):  # класс для листьев дерева, у него нет потомков, но есть значение символа
    def walk(self, code, acc):
        # потомков у листа нет, по этому для значения мы запишем построенный код для данного символа
        code[self.char] = acc or "0"  # если строка длиной 1 то acc = "", для этого случая установим значение acc = "0"

def huffman_encode(s):  # функция кодирования строки в коды Хаффмана
    h = []  # инициализируем очередь с приоритетами
    for ch, freq in Counter(s).items(): # постоим очередь с помощью цикла, добавив счетчик, уникальный для всех листьев
        h.append((freq, len(h), Leaf(ch)))  # очередь будет представлена частотой символа, счетчиком и самим символом
    heapq.heapify(h)  # построим очередь с приоритетами
    count = len(h) # инициализируем значение счетчика длиной очереди
    while len(h) > 1:  # пока в очереди есть хотя бы 2 элемента
        freq1, _count1, left = heapq.heappop(h)  # вытащим элемент с минимальной частотой - левый узел
        freq2, _count2, right = heapq.heappop(h)  # вытащим следующий элемент с минимальной частотой - правый узел
        # поместим в очередь новый элемент, у которого частота равна суме частот вытащенных элементов
        heapq.heappush(h, (freq1 + freq2, count, Node(left, right))) # добавим новый внутренний узел у которого
                                                                     # потомки left и right соответственно
        count += 1  # инкрементируем значение счетчика при добавлении нового элемента дерева
    code = {}  # инициализируем словарь кодов символов
    if h:  # если строка пустая, то очередь будет пустая и обходить нечего
        [(_freq, _count, root)] = h  # в очереди 1 элемент, приоритет которого не важен, а сам элемент - корень дерева
        root.walk(code, "")  # обойдем дерева от корня и заполним словарь для получения кодирования Хаффмана
    return code  # возвращаем словарь символов и соответствующих им кодов

def main():
    s = input()  # читаем строку длиной  до 10**4
    code = huffman_encode(s)  # кодируем строку
    encoded = "".join(code[ch] for ch in s)  # отобразим закодированную версию, отобразив каждый символ
                                             # в соответствующий код и конкатенируем результат
    print(len(code), len(encoded))  # выведем число символов и длину закодированной строки
    for ch in sorted(code): # обойдем символы в словаре в алфавитном порядке с помощью функции sorted()
        print("{}: {}".format(ch, code[ch]))  # выведем символ и соответствующий ему код
    print(encoded)  # выведем закодированную строку

if __name__ == "__main__":
    main()

Теперь можем выполнить проверку нашего алгоритма, для этого напишем функцию декодирования строки и функцию тестирования. В функции тестирования будем генерировать строку произвольных символов произвольной длины.

def huffman_decode(encoded, code):  # функция декодирования исходной строки по кодам Хаффмана
    sx =[]  # инициализируем массив символов раскодированной строки
    enc_ch = ""  # инициализируем значение закодированного символа
    for ch in encoded:  # обойдем закодированную строку по символам
        enc_ch += ch  # добавим текущий символ к строке закодированного символа
        for dec_ch in code:  # постараемся найти закодированный символ в словаре кодов
            if code.get(dec_ch) == enc_ch:  # если закодированный символ найден,
                sx.append(dec_ch)  # добавим значение раскодированного символа к массиву раскодированной строки
                enc_ch = ""  # обнулим значение закодированного символа
                break
    return "".join(sx)  # вернем значение раскодированной строки


def test(n_iter=100):  # добавим тест для проверки алгоритма
    import random  # нам понадобится генератор случайных чисел
    import string  # модуль для работы со строками, чтобы получить значения символов по их коду

    # сгененрируем строку из ascii-символов
    for i in range(n_iter):  # тест включает краевые случаи с пустой строкой и строкой из 1 символа
        length = random.randint(0, 32)  # сгеренируем код символа
        s = "".join(random.choice(string.ascii_letters) for _ in range(length)) # получим символ по коду и добавим к строке
        code = huffman_encode(s)  # выполним кодирование строки
        encoded = "".join(code[ch] for ch in s)  # получим закодированную строку
        assert huffman_decode(encoded, code) == s  # раскодируем строку и сравним ее с исходной строкой

P.S. Еще, если вы не заметили, я сделал пагинацию страничек моего блога по 5 статей на страничку, так как статей уже довольно много и они начинают ощутимо по времени грузиться. Также добавил немного снега в преддверии новогодних праздников. Надеюсь вам нравится.